Comment la mise en œuvre simple suivante de SUM code> est-elle plus rapide? private long sum( int [] a, int begin, int end ) {
if( a == null ) {
return 0;
}
long r = 0;
for( int i = begin ; i < end ; i++ ) {
r+= a[i];
}
return r;
}
22 Réponses :
en C ++, le suivant:
int* a2 = a + end - 1;
for( int i = -(end - begin - 1); i <= 0 ; i++ )
{
r+= a2[i];
}
Selon le processeur et le cache, cela pourrait réellement être plus lent. Moins d'instructions ne correspond pas toujours plus de vitesse.
@myers: Qu'est-ce qui peut être réellement plus lent ici? Nous traversons les mêmes articles, juste en arrière.
Les préfeteurs supposent souvent que les accès à la mémoire seront séquentiels. Je n'ai pas de temps (ou de connaissances suffisamment avancées) pour élaborer, mais je pense que c'est un concept googlable.
@myers: OK, regarde le deuxième exemple
Je serais surpris si ceux-ci font une différence du tout
(Aussi pour Java, Hotspot ne prend pas la peine de faire une charge d'optimisations pour les boucles à l'envers, car les personnes saines ne les écrivent pas (pour une raison pour une raison d'une raison, le point chaud est assez intelligent des boucles avant).).
Je ne crois pas que le problème soit dans le code que vous avez fourni, mais la solution plus grande doit être sous-optimale. Ce code semble bon calculer la somme d'une tranche de la matrice, mais ce n'est peut-être pas ce dont vous avez besoin pour résoudre tout le problème.
Si vous utilisez C ou C ++ et développez-vous pour les systèmes de bureau modernes et que vous êtes disposé à apprendre un assembleur ou d'apprendre à propos de GCC intrinsics, vous pouvez utiliser instructions SIMD .
Cette bibliothèque est un exemple de ce qui est possible pour float et Double Les tableaux, des résultats similaires doivent être possibles pour l'arithmétique entier car SSE dispose également d'instructions entier.
Ce code est assez simple que, sauf si Edit: Il semble que la plupart de ce qui est ci-dessus a peu à voir avec la vraie question. Il est un peu petit, donc il peut être difficile à lire, mais j'ai essayé juste en utilisant A est tout à fait petit, il va probablement être limité principalement par bande passante mémoire. En tant que tel, vous ne pouvez probablement pas espérer un gain significatif en travaillant sur la partie qui résume elle-même (par exemple, déroulant la boucle, comptant au lieu de mettre en place, en exécutant des sommes en parallèle - à moins que ce soit sur des processeurs séparés, chacun avec ses propre accès à la mémoire). Le plus gros gain proviendra probablement d'émettre des instructions de précharge afin que la plupart des données seront déjà dans le cache au moment où vous en avez besoin. Le reste sera juste (au mieux) que la CPU se dépêche de plus, de sorte qu'il attend plus longtemps.
std :: Accumulez () pour l'addition initiale, et il semblait penser que tout allait bien:
Probablement vrai que les unités entière sur la plupart des processeurs sont si rapides maintenant que même les instructions de SIMD ne font pas grand chose à moins que vous ne soyez beaucoup de chiffres. Je soupçonne que les stands de pipeline possibles des instructions de SSE mal commandés ralentissaient suffisamment la version SIMD pour ne pas offrir beaucoup de vitesse sur la solution naïve.
+1. Dans D, ils ont vectorisé des opérations ops qui utilisent des instructions de SSE. Ils sont un beau sucre syntaxique, mais pas plus rapide que d'utiliser une vieille boucle, à l'exception de très petits tableaux.
Probablement le plus rapide que vous puissiez obtenir serait d'avoir votre ensemble de 16 octets d'intensité alignée, flux 32 octets en deux La plus grande question est de savoir pourquoi une addition simple est un candidat digne d'optimisation.
EDIT: Je vois que c'est surtout un exercice académique. Peut-être que je vais lui donner un aller demain et poster des résultats ... __ m128i variables (VC ++) et appelez _mm_add_epi32 (à nouveau , un VC ++ intrinsèque) sur les morceaux. Réutilisez l'un des morceaux pour continuer à y ajouter et sur l'extrait de chunk final vos quatre intens et les ajoutez de la manière façonnée.
Si cela est basé sur le problème de l'échantillon réel, votre problème n'est pas la somme. Votre problème est la manière dont vous calculez l'indice d'équilibre. Une implémentation naïve est O (n ^ 2). Une solution optimale est beaucoup mieux mieux.
Une solution optimale est O (n), comme vous le dites. Étant donné que l'échantillon est écrit / testé en ligne, je doute sérieusement qu'il teste les minuties de la pipeline et du déroulement de la boucle.
@San, même alors cela serait dominé par des accès à la mémoire lorsque vous échouez. :)
MSN, des idées sur une implémentation qui n'est pas O (n ^ 2)
@Solution yogi: Je l'ai fait: P (ne sachant pas exactement comment, mais j'ai fait: p) J'ai fait ce que je fais pour le travail, si j'ai une solution de travail et que je prends trop longtemps, je modifie la solution pour donner le même résultat avec différentes étapes et cela fonctionnait! :)
Oscar, j'étais tellement bugé que je ne pouvais pas le résoudre dans O (n). En pensant plus à ce sujet, enfin, j'ai également trouvé un moyen de le résoudre dans O (n). Il est satisfaisant de trouver une solution! :)
Juste une pensée, je ne sais pas si l'accès au pointeur est directement plus rapide
in c # 3.0, mon ordinateur strong> et mon système d'exploitation strong> est plus rapide aussi longtemps que vous pouvez garantir que 4 numéros consécutifs ne débordent pas la gamme d'int, probablement Parce que la plupart des ajouts sont effectués en utilisant des mathématiques 32 bits.
Cependant, l'utilisation d'un meilleur algorithme offre généralement une vitesse supérieure à une vitesse supérieure à une micro-optimisation. temps pour un réseau d'éléments de 100 millirs: p> 4999912596452418 -> 233 ms (somme) p> 4999912596452418 - > 126ms (Sum2) P> private static long sum2(int[] a, int begin, int end)
{
if (a == null) { return 0; }
long r = 0;
int i = begin;
for (; i < end - 3; i+=4)
{
//int t = ;
r += a[i] + a[i + 1] + a[i + 2] + a[i + 3];
}
for (; i < end; i++) { r += a[i]; }
return r;
}
Quelques astuces:
Utilisez un profileur pour identifier où vous dépensez beaucoup de temps.
Écrivez de bons tests de performance afin que vous puissiez dire l'effet exact de chaque changement que vous faites. Gardez des notes prudentes.
S'il s'avère que le goulot d'étranglement est la vérification pour vous assurer que vous êtes une adresse légale à l'intérieur de la matrice, vous pouvez garantir que le début et la fin sont en fait à l'intérieur de la matrice, puis envisagez de réparer le Array, faisant un pointeur sur le tableau et faire l'algorithme dans des pointeurs plutôt que des tableaux. Les pointeurs sont dangereux; Ils ne dépensent pas de temps à vérifier pour vous assurer que vous êtes toujours à l'intérieur de la matrice. Par conséquent, ils peuvent donc être un peu plus rapides. Mais vous prends la responsabilité alors de vous assurer que vous ne corrompiez pas tous les octets de la mémoire dans l'espace d'adresses.
Je ne pense pas que votre problème soit avec la fonction qui résume la matrice, c'est probablement que vous sommez la voie à la matrice à fréquemment. Si vous émettez simplement la matrice entière une fois, puis détournez la matrice jusqu'à ce que vous trouviez le premier point d'équilibre, vous devez réduire suffisamment le temps d'exécution.
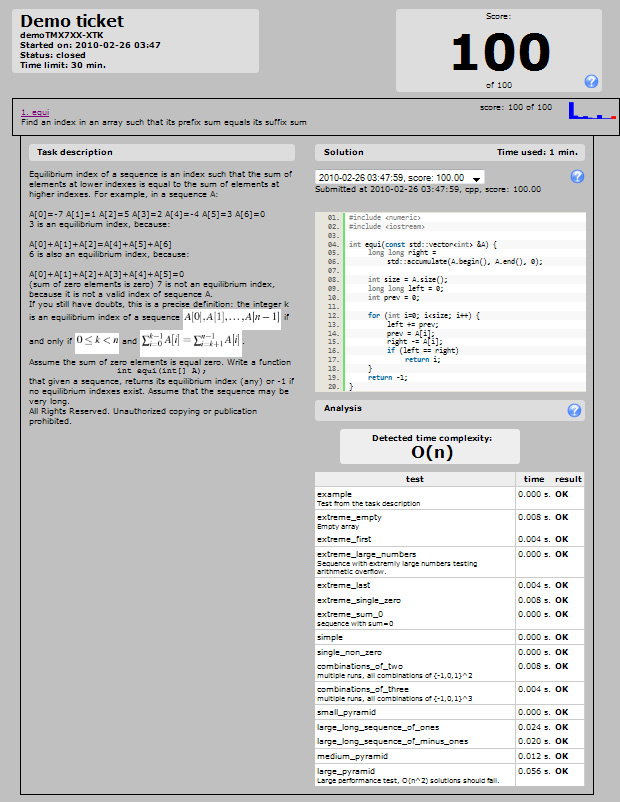
int equi ( int[] A ) {
int equi = -1;
long lower = 0;
long upper = 0;
foreach (int i in A)
upper += i;
for (int i = 0; i < A.Length; i++)
{
upper -= A[i];
if (upper == lower)
{
equi = i;
break;
}
else
lower += A[i];
}
return equi;
}
Yeap, c'est exactement ce que j'ai fait. Initialement, j'ai eu était: si (somme (0, i) == somme (i, fin)) renvoie i mais qui a invoqué trop de temps à somme donc je Changez-le pour: total = somme (a) et à l'intérieur du pour: if (actuel = courant total) {retour i}
changements à int Equi = -1; Au lieu de 0 et vous obtiendrez un 100/100 avec cette solution.
J'ai fait la même implémentation naïve et voici ma solution O (n). Je n'ai pas utilisé la méthode de somme ienumérable car elle n'était pas disponible à la codité. Ma solution ne vérifie toujours pas le débordement au cas où l'entrée dispose de grandes numéros, de sorte que cela échoue à un test particulier sur la codité. 
+1 super !!! ... Qu'est-ce que "combinaisons_of_two" Tout sur? Sur le "extreme_lange_numbers" est très très très facile, il suffit d'utiliser long dans la méthode gettotal au lieu de int et vous 'll aura 100%;)
Je ne sais pas quels sont ces cas. Mais je fais des chèques initiaux par ex. Si la longueur du tableau est zéro ou 1, le code renvoie immédiatement l'index d'équilibre. Peut-être que c'est pourquoi mon minutage moyen est de 0,072S où votre minutage moyen est de 0,244. C'était un exercice amusant, merci d'avoir honoré! :)
Cela ne vous aidera pas avec un algorithme O (N ^ 2), mais vous pouvez optimiser votre somme.
Lors d'une entreprise précédente, nous avons eu Intel viennent de venir et de nous donner des conseils d'optimisation. Ils avaient une astuce non évidente et un peu fraîche. Remplacer: avec pourquoi il est plus rapide:
Dans la mise en œuvre initiale, votre variable R est un goulot d'étranglement. Chaque fois que traversez la boucle, vous devez tirer des données de la mémoire de mémoire A (qui prend quelques cycles), mais vous ne pouvez pas effectuer de multiples tirettes en parallèle, car la valeur de R dans la prochaine itération de la boucle dépend de la valeur. de r dans cette itération de la boucle. Dans la deuxième version, R1, R2, R3 et R4 sont indépendants, le processeur peut donc hyperthread leur exécution. Seulement à la fin, se réunissent-ils.
{In Pascal + Assembly}
{$ASMMODE INTEL}
function equi (A : Array of longint; n : longint ) : longint;
var c:Longint;
label noOverflow1;
label noOverflow2;
label ciclo;
label fine;
label Over;
label tot;
Begin
Asm
DEC n
JS over
XOR ECX, ECX {Somma1}
XOR EDI, EDI {Somma2}
XOR EAX, EAX
MOV c, EDI
MOV ESI, n
tot:
MOV EDX, A
MOV EDX, [EDX+ESI*4]
PUSH EDX
ADD ECX, EDX
JNO nooverflow1
ADD c, ECX
nooverflow1:
DEC ESI
JNS tot;
SUB ECX, c
SUB EDI, c
ciclo:
POP EDX
SUB ECX, EDX
CMP ECX, EDI
JE fine
ADD EDI, EDX
JNO nooverflow2
DEC EDI
nooverflow2:
CMP EAX, n
JA over
INC EAX
JMP ciclo
over:
MOV EAX, -1
fine:
end;
End;
private static int equi ( int[] A ) {
if (A == null || A.length == 0)
return -1;
long tot = 0;
int len = A.length;
for(int i=0;i<len;i++)
tot += A[i];
if(tot == 0)
return (len-1);
long partTot = 0;
for(int i=0;i<len-1;i++)
{
partTot += A[i];
if(partTot*2+A[i+1] == tot)
return i+1;
}
return -1;
}I considered the array as a bilance so if the equilibrium index exist then half of the weight is on the left. So I only compare the partTot (partial total) x 2 with the total weight of the array.
the Alg takes O(n) + O(n)
J'ai marqué 100% pour celui-ci:
int equi (int[] A)
{
if (A == null) return -1;
long sum0 = 0, sum1 = 0;
for (int i = 0; i < A.Length; i++) sum0 += A[i];
for (int i = 0; i < A.Length; i++)
{
sum0 -= A[i];
if (i > 0)
{
sum1 += A[i - 1];
}
if (sum1 == sum0) return i;
}
return -1;
}
Voici une pensée:
probablement pas parfait mais qu'il passe de toute façon :) peut ' T Sense que je suis un grand fan de la codilité, c'est une idée intéressante, mais j'ai trouvé les exigences un peu trop vagues. Je pense que je serais plus impressionné s'ils vous ont donné des exigences + une suite de tests unitaires qui testent ces exigences et alors vous ont demandé d'écrire du code. C'est ainsi que la plupart du TDD survient de toute façon. Je ne pense pas que ça aveugle gagne vraiment autre chose que de leur permettre de jeter dans des cas de coin.
100% correction et performances de ce code est testée
Private Function equi(ByVal A() As Integer) As Integer
Dim index As Integer = -1
If A.Length > 0 And Not IsDBNull(A) Then
Dim sumLeft As Long = 0
Dim sumRight As Long = ArraySum(A)
For i As Integer = 0 To A.Length - 1
Dim val As Integer = A(i)
sumRight -= val
If sumLeft = sumRight Then
index = i
End If
sumLeft += val
Next
End If
Return index
End Function
Voici ma solution et j'ai marqué 100%
Nécessite système.Linq; Mais belle réponse!
J'ai aimé cette solution, mais je ne pense pas que la complexité du temps pire du cas est O (n) premier double somme = A.Sum (d => (double) d); est O (n) alors vous en avez un de plus pour lequel le faire O (2n), ai-je raison?
@Tarekaboelkheir O (2n) = O (n). C'est comme ça que Big Oh travaille.
Cette solution est 100% correcte mais elle me dérange avec le style XD. Quel est le point de sinon ici? si (LEFTSUM == Sum-Leftsum-A [i]) retour I; LEFTSUM + = A [I] est suffisant: p
Cela m'a gagné 100% en JavaScript: 
Voici ma réponse avec des explications sur la façon d'y aller. Il vous obtiendra 100%
class Solution
{
public int solution(int[] A)
{
long sumLeft = 0; //Variable to hold sum of elements to the left of the current index
long sumRight = 0; //Variable to hold sum of elements to the right of the current index
long sum = 0; //Variable to hold sum of all elements in the array
long leftHolder = 0; //Variable that holds the sum of all elements to the left of the current index, including the element accessed by the current index
//Calculate the total sum of all elements in the array and store it in the sum variable
for (int i = 0; i < A.Length; i++)
{
//sum = A.Sum();
sum += A[i];
}
for (int i = 0; i < A.Length; i++)
{
//Calculate the sum of all elements before the current element plus the current element
leftHolder += A[i];
//Get the sum of all elements to the right of the current element
sumRight = sum - leftHolder;
//Get the sum of all elements of elements to the left of the current element.We don't include the current element in this sum
sumLeft = sum - sumRight - A[i];
//if the sum of the left elements is equal to the sum of the right elements. Return the index of the current element
if (sumLeft == sumRight)
return i;
}
//Otherwise return -1
return -1;
}
}
Ceci peut être vieux, mais voici une solution à Golang avec une vitesse de passage de 100%:
Permettez-vous l'assemblage en ligne en C ++?
Personne ne peut commenter la vitesse à moins d'expliquer quelle langue et quelle plate-forme vous utilisez. Comme mmyers dit, s'il s'agit de C ++, vous pourriez assembler un assemblage. Si c'est C # la méthode intégrée énumérable.sum () peut être plus rapide, qui sait. Je suis sûr que Java a aussi de bonnes trucs.
@myers: Pas autant. Plus probablement dans l'optimisation figure sur la partie d'algorithme plutôt que dans la partie de mise en œuvre: - / (si cela a même logement)
@Ocar: Si l'assemblage est autorisé, en fonction de la plate-forme cible, les instructions de vecteur SSE pourraient être utilisées pour le parallementer.
Sauf si vous souhaitez diviser la tâche en
Num_Cores Les threads de la taille d'une taille suffisamment grande pour bénéficier malgré les frais généraux dans l'initialisation du fil, je pense que vous êtes à peu près fait.En passant, lorsque vous dites "fondamentalement (je pense), c'est parce que cette mise en œuvre de la somme", vous voulez vraiment dire "je l'ai profilée et a constaté qu'il dépense 40% de son temps dans cette mise en œuvre de la somme", n'est-ce pas? Parce que sinon, c'est un exercice assez inutile. :)
Je ne pouvais pas non plus trouver une solution O (n) en 30 minutes. Donc, j'ai certainement besoin d'améliorer. Je suis proposé une solution O (n ^ 2) dans 5 minutes. Nous devons nous rappeler une chose, si vous écrivez des applications LOB, c'est OKIE si votre solution est O (n ^ 2) si n est faible et le temps de livrer est plus important.
J'en ai un à O (n), mais je n'ai pas vérifié tous les cas de bord et je n'ai pas utilisé de longs. Je n'ai qu'un 50.: P (mais j'ai utilisé moins de la moitié du temps imparti, donc au moins en théorie, j'aurais pu résoudre tous ces problèmes.)
C'est un exemple parfait de la raison pour laquelle les gens doivent profiler. Tout comme les gens autour d'ici, disent toujours ce que vous pensez être le point de starter n'est pas souvent. Vous ne savez tout simplement pas avant de mesurer.
@Évan, vous n'avez pas besoin de profiler si vous savez ce que vous faites. Cela transformera cette conversation en signe de drapeau, mais cela m'a fallu 30 secondes pour comprendre pourquoi cela pourrait être lent (O (n ^ 2)) et comment le faire O (n). Bien que je suppose que cela signifierait un profil si vous ne savez pas ce que vous faites.
C'est comme ça que j'ai profilé (avec un profileur BTW), je fais une version de 2 threads de la méthode SUM et je l'ai vu avoir pris à peu près au même moment. J'ai ajouté des journaux d'impression et j'ai vu que je créais jusqu'à 2k threads (pas en même temps) pour mon tableau 1k. C'est quand je savais que j'appelle la méthode
somme trop souvent. Ce qui me conduit à cette conclusion (je ne suis pas aussi intelligent que MSN et cela me prend plus de 30 secondes) était l'essai en échec dans de grands ensembles. Sinon, je n'irais pas aussi loin.